T.C. - MILDRED ANDREA CANO VILLATORO

TEORÍA DE CONJUNTOS

¿Qué es un conjunto? 

Es muy importante en todas las ramas de las matemáticas porque es un grupo de elementos u objetos especificados en tal forma que se puede afirmar con certeza si cualquier objeto dado pertenece o no a la agrupación.

Un conjunto es:

• Una lista
• Colección 
• Clase de objetos bien definidos (Números, personas, letras, ríos, etc.)

 Notación de conjuntos:

• Denotar conjuntos por letras mayúsculas (A, B, C, X, Y, Z...).
• Los elementos de los conjuntos se representan por letras minúsculas (a, b, c, x, y, z...).
• Al definir un conjunto por efectiva enumeración de los elementos, por ejemplo, el A, que consiste en los números 1, 3, 7 y 10, se escribe

                                     A={1, 3, 7, 10}

Se escriben los elementos separados por comas y encerrándolos en llaves {}.

• La Fórmula Tabular  de un conjunto. Se define un conjunto enunciando propiedades que deben tener sus elementos como por ejemplo, el B, conjuntos de todos los números pares, entonces se emplea una letra, por lo general x, para representar un elemento cualquiera y se escribe:

                                       B= {x/x es para}

Lo que se lee "B es el conjunto de los números x tales que x es par". Se dice que ésta es la forma de definir para una comprensión constructiva de un conjunto. 

• Si un objeto x es el elemento de un conjunto A, es decir A contiene a x como uno de sus elementos, se escribe:

                                             x ∈ A

se lee, "x pertenece a A" o "x está en A".

• Si un objeto x no es el elemento de un conjunto A, es decir , si A no contiene a x entres sus elementos, se escribe:

                                              x ∉ A

se lee, "x no pertenece a A" o "x no está en A".

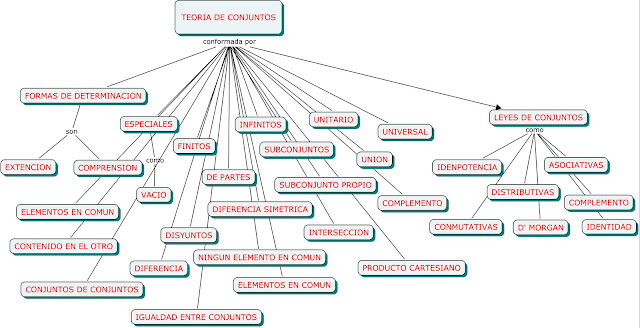
Existen cuatro formas de enunciar a los conjuntos:

 1) Por extensión o enumeración: los elementos son encerrados entre llaves y separados por comas. Es decir, el conjunto se describe listando todos sus elementos entre llaves. 

2) Por comprensión: los elementos se determinan a través de una condición que se establece entre llaves. En este caso se emplea el símbolo | que significa “tal que". En forma simbólica es: A = { x P(x) }= {x1 x, 2 x, 3 , ⋅⋅⋅ x, n } que significa que el conjunto A es el conjunto de todos los elementos x tales que la condición P(x) es verdadera, como 1 2 3 x x, x, , etc. . 

3) Diagramas de Venn: son regiones cerradas que sirven para visualizar el contenido de un conjunto o las relaciones entre conjuntos 2.

 4) Por descripción verbal: Es un enunciado que describe la característica que es común para los elementos.  

CONJUNTOS CON NOMBRES ESPECÍFICOS 

• Un conjunto vacío o nulo es aquel que no posee elementos. Se denota por: φ o bien por { }. El conjunto vacío siempre forma parte de otro, así que es subconjunto de cualquier conjunto.  

Ejemplo:

φ = { x /x son los dinosaurios que viven en la actualidad } 

{ }= { x /x son los hombres mayores de 300 años } 

φ = { x /x son números positivos menores que cero} 

• Un conjunto universal es aquel que contiene a todos los elementos bajo consideración. Se denota por U . Gráficamente se le representará mediante un rectángulo.  

Ejemplos:

 U = { x /x son los días de la semana }= {lunes,martes,miércoles, jueves,viernes,sábado ,domingo } 

A = { x /x son los días de la semanainglesa}= {lunes,martes,miércoles, jueves,viernes} 

B = { x /x son los días del fin de semana }= {sábado,domingo }

 C = { x /x son los días de la semana con menos de siete letras}= {lunes,martes, jueves,sábado} 

Nótese cómo: A ⊂ U , B ⊂ U , C ⊂ U

• Un conjunto finito es aquel cuyos elementos pueden ser contados. 

Ejemplo:

J = { x /x es el número de un día del mes de junio }

• Un conjunto infinito es aquel cuyos elementos no pueden ser contados, es decir, su cardinalidad no está definida. 

Ejemplos:

N = {1,3,5,7,9,11,⋅⋅⋅}

 M = {2,4,6,8,10,12,⋅⋅⋅}

 Q = { x /x es la cantidad de puntos en una línea } 

• Dos conjuntos son iguales si tienen exactamente los mismos elementos. Se denota por el símbolo = . 

Ejemplo:

 R = {1,2,3,4,5,6,7,8,9,0} 

S = { x /x es un dígito } 

R = S

• Dos conjuntos son desiguales si por lo menos difieren en un elemento, es decir, si no tienen exactamente los mismos elementos. Se denota por el símbolo ≠ .

• Dos conjuntos son equivalentes si tienen la misma cantidad de elementos, es decir, si poseen la misma cardinalidad. Se denota por el símbolo ≈ .

 Ejemplos:

W = {x /x son las estaciones del año } 

Z = {x /x es un punto cardinal } 

η(W ) = 4 

η(Z) = 4 

W ≈ Z

Nota: Cuando los conjuntos son equivalentes existe una correspondencia uno a uno o biunívoca. Esto significa que se puede establecer una relación que asocie a cada elemento del primer conjunto con un único elemento del segundo conjunto sin que sobren elementos en ningún conjunto.

PROPIEDADES DE LOS CONJUNTOS 

Sean los conjuntos ,A ,B C dentro del universo U . Las seis propiedades que rigen las operaciones con esos conjuntos son las siguientes: 

1. Propiedades de identidad: 

A∪ φ = A 

A∪U = U 

A∩U = A 

A∩φ = φ 

2. Propiedades de idempotencia:

 A∪ A = A 

A∩ A = A 

3.Propiedades de complemento:

 A∪ 'A = U 

A∩ 'A = φ 

4. Propiedades asociativas: 

(A∪ B)∪C = A∪ (B ∪C)

 (A∩ B)∩C = A∩ (B ∩C) 

5. Propiedades conmutativas:

A∪ B = B ∪ A 

A∩ B = B ∩ A 

6. Propiedades distributivas:

 A∪ (B ∩C) = (A∪ B)∩(A∪C)

 A∩(B ∪C) = (A∩ B)∪(A∩C)

OPERACIONES ENTRE CONJUNTOS

 Además de relacionar los conjuntos a través de la contenencia y la igualdad, se pueden crear operaciones entre conujuntos.

-Unión de conjuntos:

Supongamos que tenemos los conjuntos  $M$ y $N$ definidos como se muestra en la siguiente figura:

Podemos crear otro conjunto conformado con los elementos que pertenezcan a $M$ o a $N$.  A este nuevo conjunto le llamamos unión de $M$ y $N$, y lo notamos de la siguiente manera:$M\cup N$.  En la imagen de abajo puedes observar el resultado de unir los conjuntos $M$ y $N$.

Al elegir qué elementos estarán en la unión de nuestros conjuntos $M$ y $N$, debes preguntarte cuáles están en el conjunto $M$“o” en el conjunto $N$. 

 El resultado de la operación será el conjunto conformado por todos los elementos del conjunto universal U${\displaystyle U}$, que cumplan la condición de estar en uno o en otro.   Tenemos en este caso: $M\cup N=\{a,c,b,g,e,1\}$

-Intersección de conjuntos:

Sigamos tomando como ejemplo los conjuntos $M$ y $N$ definidos anteriormente.  Podemos determinar un nuevo conjunto conformado por los elementos que nuestros conjuntos $M$y $N$ tienen en común.  A este nuevo conjunto le llamamos intersección de $M$ y $N$ y lo notamos de la siguiente manera: $M\cap N$.

Para determinar que elementos pertenecen a la intersección de los conjuntos $M$ y $N$ te puedes preguntar qué elementos están en $M$ “y” en  $N$.  Todos los elementos del conjunto $U$ que cumplan esta condición deberán estar en el conjunto $M\cap N$.  En la figura de la arriba podemos ver la intersección de nuestros conjuntos $M$ y $N$, tenemos que $M\cap N=\left\{b\right\}$.

-Diferencia de conjuntos:

Además de la unión y la intersección podemos realizar la diferencia de conjuntos.  En este caso se deben seleccionar los elementos de un conjunto que no estén en el otro.  Por ejemplo, si realizas la operación $M$ menos $N$, debes seleccionar los elementos de $M$ que no están en $N$.  Representamos la diferencia M menos N así: $M\backslash N$.  Observa que en este caso $M\backslash N=\{a,c\}$.

-Diferencia Simétrica de conjuntos:

Que el nombre esta operación no te alarme, también es muy sencilla.  En esta ocasión se deben escoger los elementos de $M$ que no están en $N$, y los elementos de $N$ que no están en $M$.  Puedes ver el resultado de ladiferencia simétrica entre $M$ y $N$ en la figura de la izquierda.  Representamos la diferencia simétrica a través del símbolo $\Delta$.  En el caso de nuestros conjuntos $M$ y $N$tenemos: $M\Delta N=\{a,c,g,1,e\}$.

-Complemento de un conjunto:

  Se dice que el complemento de $M$ es el conjunto conformado por todos los elementos del conjunto universal $U$, que no pertenecen al conjunto $M$.  Es común usar los símbolos $M^c$, $\overline{M}$ o $M\text{'}$ para representar el complemento del conjunto $M$, nosotros usaremos el símbolo $M^c$.  En nuestro caso tenemos $M^c=\{j,f,g,1,e,i,h\}$ y $N^c=\{i,h,j,f,a,c\}$.

REPRESENTACIÓN GRÁFICA DE CONJUNTOS: 

1. Los conjuntos se pueden representar gráficamente mediante curvas cerradas, conocidas con el nombre de diagramas de venn, y para poder interpretarlos correctamente hay que observar lo siguiente:
elementos que pertenecen al conjunto se representan por puntos interiores a la curva.

2. Los elementos que no pertenecen al conjunto se representan por puntos exteriores a la curva.

3. Ningún punto se representa sobre la curva.

4. El conjunto referencial R se representan por un rectángulo para diferenciarlos de los otros diagramas.

si R = (1,2,3,4,5,6,7,8) y A= (4,5,6)

Los conjuntos son de suma importancia para la toma de decisiones en nuestra vida académica, monetaria e intelectual, en ellos podemos encontrar respuesta a los problemas que se nos presenten al hacer una Auditoría, realizándo un proceso ordenado y sistemático.