"ANÁLISIS DIMENSIONAL"
El análisis dimensional es una parte de la física que estudia la forma como se relacionan las magnitudes derivadas con las fundamentales. Tal estudio se hace básicamente para descubrir valores numéricos, a los que los llamaremos "Dimensiones", los cuales aparecen como exponentes de los símbolos de las magnitudes fundamentales.
Fines del análisis dimensional:
- El análisis dimensional sirve para expresar (relacionar) las magnitudes derivadas en términos de las fundamentales.
- Sirven para comprobar la veracidad o falsedad de las fórmulas físicas, haciendo uso del principio de homogeneidad dimensional.
- Sirven para deducir nuevas fórmulas a partir de datos experimentales. (Fórmulas Empíricas).
Magnitudes y unidades:
Todo aquello que sea susceptible de aceptar una comparación con otra de su misma especie, es una magnitud (con la consideración de que ésta debe ser inmaterial). Así por ejemplo son magnitudes, la longitud, la masa, el tiempo, el área, el volumen, etc.
Llamamos unidad de medida a aquella cantidad elegida como patrón de comparación. Una misma magnitud puede tener varias unidades de medida.
Clasificación de las magnitudes:
| Por su origen | Por su naturaleza |
|
|
Magnitudes fundamentales:
Son todas aquellas que tienen la particular característica de estar presente en todos o casi todos los fenómenos físicos, y además sirven de base para escribir o representar las demás magnitudes.
| SISTEMA INTERNACIONAL DE UNIDADES (S.I.) | ||
| Magnitud | Símbolo | Unidad Básica (Símbolo) |
| Longitud. | L | Metro (m) |
| Masa. | M | Kilogramo (kg) |
| Tiempo. | T | Segundo (s) |
| Intensidad de corriente eléctrica. | I | Ampere o Amperio (A) |
| Intensidad Luminosa. | J | Candela (cd) |
| Temperatura Termodinámica. |
q
| Kelvin (K) |
| Cantidad de Sustancia. | N | Mol (mol) |
| MAGNITUDES AUXILIARES COMPLEMENTARIAS O SUPLEMENTARIAS | |
| Nombre | Unidad Básica (Símbolo) |
| Ángulo Plano. | Radian (rad). |
| Ángulo Sólido. | Estereorradián (sr). |
Magnitudes derivadas:
En número es el grupo más grande (ilimitado) en el cada uno puede definirse por una combinación de magnitudes fundamentales y/o auxiliares. Estas combinaciones se consiguen mediante las operaciones de multiplicación, división, potenciación y radicación. Por lo tanto toda magnitud derivada tendrá la siguiente forma: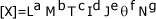 
; donde los exponentes numéricos: a, b, c, d, e, f, g, se conocen como dimensiones.
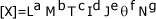; donde los exponentes numéricos: a, b, c, d, e, f, g, se conocen como dimensiones.
Ejemplo: área, Volumen, velocidad, aceleración, fuerza, trabajo, energía, calor, etc.
Magnitudes escalares:
Son aquellas magnitudes que quedan perfectamente determinadas o bien definidas con sólo conocer su valor numérico o cantidad y su respectiva unidad de medida.
Ejemplo: área, volumen, longitud, tiempo, trabajo, energía, calor, etc.
Magnitudes vectoriales:
Son aquellas magnitudes que además de conocer su valor numérico y su unidad, se necesita la dirección y sentido para que dicha magnitud quede perfectamente definida o determinada.
Ejemplo: Velocidad, aceleración, fuerza, gravedad, etc.
Múltiplos y submúltiplos:
| MÚLTIPLOS | SUBMÚLTIPLOS | ||
| Nombre y Símbolo | Factor | Nombre y Símbolo | Factor |
| Yotta (Y) | 10 24 | Deci (d) | 10 -1 |
| Zeta (E) | 10 21 | Centi (c) | 10 -2 |
| Exa (E) | 10 18 | Mili (m) | 10 -3 |
| Peta (P) | 10 15 | Micro (m) | 10 -6 |
| Tera (T) | 10 12 | Nano (n) | 10 -9 |
| Giga (G) | 10 9 | Pico (p) | 10 -12 |
| Mega (M) | 10 6 | Femto (f) | 10 -15 |
| Kilo (k) | 1000 | Atto (a) | 10 -18 |
| Hecto (h) | 100 | Zepto (z) | 10 -21 |
| Deca (da) | 10 | Yocto (y) | 10 -24 |
Ecuaciones dimensionales:
Llamadas también "fórmulas dimensionales", son expresiones matemáticas que colocan a lasmagnitudes derivadas en función de las fundamentales, utilizando para ello las reglas básicas del álgebra, excepto la suma y resta.
Notación:
A: se lee magnitud "A"; [A]: se lee Ecuación Dimensional de "A".
Formulas para las siguientes figuras:
No hay comentarios.:
Publicar un comentario