L. P. Andy Esaú Cobón.

.

Lógica.

Es una ciencia que estudia el lenguaje científico, su planteamiento, su organización, en entidades jerárquicas y los métodos como sus fórmulas para analizar toda forma escrita. Para comunicarse el ser humano utiliza lenguajes discursivos dichos lenguajes están llenos de partículas lógicas.

Lógica Proposicional.

Es una rama de la lógica clásica que estudia las variables proposicionales o sentencias lógicas, sus posibles implicaciones, evaluaciones de verdad y en algunos casos su nivel absoluto de verdad. Algunos autores también la identifican con la lógica matemática o la lógica simbolice, ya que utiliza una serie de símbolos especiales que lo acercan al lenguaje matemático.

Proposiciones.

Tautología: se define tautología o validez a aquella fórmula que siempre es verdadera.

Contradicción: es una proposición que siempre es falsa para todos los valores de verdad. Para cualquier valor de verdad de las proposiciones, sea cual sea el resultado de la fórmula lógica estudiada siempre va a ser falso.

Conjunción: es aquella fórmula que es falsa o verdadera. Las expresiones de las que depende la validez de los argumentos se definen constante lógicas.

Conectores.

Negación: no -> >, ~

En lógica y matemática, la negación, también llamada complemento lógico, es una operación sobre proposiciones, valores de verdad, o en general, valores semánticos. Intuitivamente, la negación de una proposición es verdadera cuando dicha proposición es falsa, y viceversa. En lógica clásica la negación está normalmente identificada con la función de verdad que cambia su valor de verdadero a falso y viceversa.

Conjunción: Y ∧, 

Solamente si las componentes de la conjunción son ciertas, la conjunción es cierta.

Disyunción: O ∨,

La disyunción solamente es falsa si lo son sus dos componentes.

Condicional: ⇒ entonces

Típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad falso sólo cuando la primera proposición es verdadera y la segunda falsa.

Bicondicional: ⇔ si solo sí.

El Bicondicional o doble implicación es un operador que funciona sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones tienen el mismo valor de verdad, y falso cuando sus valores de verdad difieren.

Proposiciones.

Variables: En el lenguaje simbólico de la lógica de proposiciones, a los enunciados simples, atómicos o elementales son los que no pueden descomponerse en otros más simples. Se les llama variables, y se escriben con las letras minúsculas del final del abecedario: “p”, “q”, “r”, “s”… para los casos particulares, o con las letras en mayúscula del principio del alfabeto cuando son casos generales: “A”, “B”, “C”, “D”…

TABLAS DE VERDAD.

Origen.

Fue desarrollada por Charles Sanders Peirce por los años 1880, pero el formato más popular es el que introdujo Ludwig Wittgenstein en su Tractatus logico-philosophicus, publicado en 1921. 
La tabla de los "valores de verdad", es usada en el ámbito de la lógica, para obtener la verdad (V) o falsedad (F), valores de verdad, de una expresión o de una proposición. Además sirven para determinar si es que un determinado esquema de inferencia es formalmente válido como un argumento, llegando a la conclusión de que este es una tautología (se habla de una tautología cuando todos los valores de la tabla mencionada son "V" o sea verdadero). 

Qué son las tablas de la verdad:

Las tablas de verdad son, por una parte, uno de los métodos más sencillos y conocidos de la lógica formal, pero la mismo tiempo también uno de los más poderosos y claros. Entender bien las tablas de verdad es, en gran medida, entender bien a la lógica formal misma. 
Fundamentalmente, una tabla de verdad es un dispositivo para demostrar ciertas propiedades lógicas y semánticas de enunciados del lenguaje natural o de fórmulas del lenguaje del cálculo proposicional:

1. Sin son tautológicas, contradictorias o contingentes
2. Cuáles son sus condiciones de verdad
3. Cuál es su rol inferencial, es decir, cuáles son sus conclusiones lógicas y de qué otras proposiciones se siguen lógicamente.

Estas tablas pueden construirse haciendo una interpretación de los signos lógicos como: no, o, y, si…entonces, sí y sólo si. La interpretación corresponde al sentido que estas operaciones tienen dentro del razonamiento. 
Puede establecerse una correspondencia entre los resultados de estas tablas y la deducción lógico matemática. En consecuencia, las tablas de verdad constituyen un método de decisión para chequear si una proposición es o no un teorema.
Para la construcción de la tabla se asignará el valor 1(uno) a una proposición cierta y 0 (cero) a una proposición falsa. 
Negación: El valor de verdad de la negación es el contrario de la proposición negada

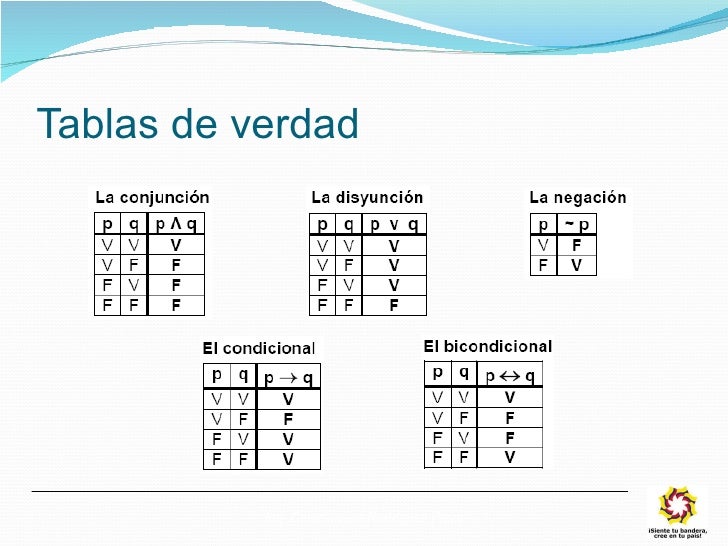
Un pequeño ejemplo de cómo se utilizan los conectores de las tablas de verdad.