"TEORÍA DE CONJUNTOS"
Un conjunto es la reunión en un todo de objetos bien definidos y diferenciales entre si, que se llaman elementos del mismo. Si a es un elemento del conjunto A se denota con la relación de pertenencia a Î A. En caso contrario, si a no es un elemento de A se denota aÏ A.
El concepto de Conjunto, está referido a reunir o agrupar personas, animales, plantas o cosas, para estudiar o analizar las relaciones que se pueden dar con dichos grupos.
Ejemplos de conjuntos:
- Æ : el conjunto vacío, que carece de elementos.
- N: el conjunto de los números naturales.
- Z: el conjunto de los números enteros.
- Q : el conjunto de los números racionales.
- R: el conjunto de los números reales.
- C: el conjunto de los números complejos.
Se puede definir un conjunto:
- por extensión, enumerando todos y cada uno de sus elementos.
- por comprensión, diciendo cuál es la propiedad que los caracteriza.
Un conjunto se suele denotar encerrando entre llaves a sus elementos, si se define por extensión,
o su propiedad característica, si se define por comprensión. Por ejemplo:
- A := {1,2,3, ... ,n}
- B := {pÎ Z | p es par}
Se dice que A está contenido en B (también que A es un subconjunto de B o que A es una parte de B),
y se denota A Í B, si todo elemento de A lo es también de B, es decir, a Î A Þ a Î B.
Dos conjuntos A y B se dicen iguales, y se denota A = B, si simultáneamente A Í B y B Í A;
esto equivale a decir que tienen los mismos elementos (o también la misma propiedad característica).
Para cualquier conjunto A se verifica que ÆÍ A y A Í A;
B Í A es un subconjunto propio de A si A ¹ Æ y B ¹ A.
El conjunto formado por todos los subconjuntos de uno dado A se llama partes de A, y se denota à (A).
Entonces, la relación B Í A es equivalente a decir B Î Ã (A).
Ejemplos:
Ejemplos:
Si A = {a,b} entonces à (A) = {Æ ,{a},{b},A}.
Si a Î A entonces {a} ÎÃ (A).
Cuando en determinado contexto se consideran siempre conjuntos que son partes de uno dado U,
se suele considerar a dicho U como conjunto universal o de referencia.
"CLASES DE JUNTOS POR SU NUMERO DE ELEMENTOS "
1. CONJUNTO UNITARIO:
Es aquel conjunto que tiene un solo elemento.
Ejemplos:

2. CONJUNTO VACIO (O NULO)
Es aquel conjunto que no tiene elementos.

Ejemplo:
A = {es el conjunto de aves que tienen 3 patas}
B = {es el conjunto de hombres con 4 piernas}
Como se habrá dado cuenta no existe ninguna ave u hombre con tres patas o cuatro piernas respectivamente, por tanto, estos conjuntos carecen de elementos y decimos que es un conjunto VACIO.
3. CONJUNTO UNIVERSAL (O UNIVERSO):

Es el conjunto que contiene, comprende o dentro del cual están todos los demás conjuntos, se le simboliza por letra U, gráficamente se le representa mediante un rectángulo en cuyo vértice (uno cualquiera) se coloca la letra U.

Si consideramos como un conjunto universal al sistema Universitario de nuestro país, entonces cada Universidad x, será elemento de dicho universo. El conjunto de libros de una biblioteca determinada, puede ser otro ejemplo, sus elementos serán cada uno de los libros de los que consta. El marco de referencia es relativo, de modo que podemos referir como conjunto universal por ejemplo al conjunto de bibliotecas de Contumazá.
4. CONJUNTO FINITO:
Es aquel cuyos elementos se pueden contar en forma usual desde el primero hasta el último. El número de sus elementos se llama cardinal de conjunto.
Ejemplos:

5. CONJUNTO INFINITO:
Si contamos no llegamos nunca a un último elemento del conjunto mencionado. A este tipo de enunciados se denominan conjuntos infinitos o indefinidos.
Ejemplo:

Ejemplo:
- 1. A = {1, 2, 3,……………..,100} (es finito)
- 2. B = {1, 2, 3,…………………….} (es infinito)
- 3. C = {……-4, -3, -2, -1, 0, 1, 2, 3, 4………} (es infinito)
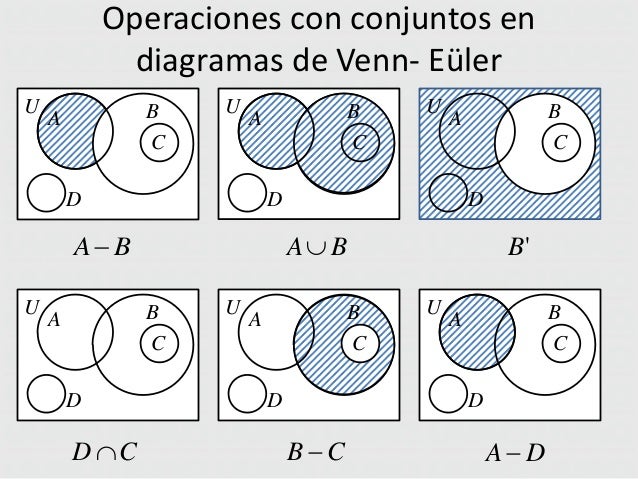
Ejemplos de operaciones con conjuntos en Diagramas de Venn:
No hay comentarios.:
Publicar un comentario