T.C josé Villatoro

Teoría de Conjuntos

Un conjunto es la reunión en un todo de objetos bien definidos y diferenciables entre si, que se llaman elementos del mismo.

Si a es un elemento del conjunto A se denota con la relación de pertenencia a Î A. 

En caso contrario, si a no es un elemento de A se denota aÏ A. 

 

Ejemplos de conjuntos: 

 

• Æ : el conjunto vacío, que carece de elementos.
• N: el conjunto de los números naturales.
• Z: el conjunto de los números enteros.
• Q : el conjunto de los números racionales.
• R: el conjunto de los números reales.
• C: el conjunto de los números complejos.

  

Se puede definir un conjunto:

• por extensión, enumerando todos y cada uno de sus elementos.
• por comprensión, diciendo cuál es la propiedad que los caracteriza.

  

Un conjunto se suele denotar encerrando entre llaves a sus elementos, si se define por extensión, 

o su propiedad característica, si se define por comprensión. Por ejemplo:

• A := {1,2,3, ... ,n}
• B := {pΠZ | p es par}

  

Se dice que A está contenido en B (también que A es un subconjunto de B o que A es una parte de B), 

y se denota A Í B, si todo elemento de A lo es también de B, es decir, a Î A Þ a Î B.

Dos conjuntos A y B se dicen iguales, y se denota A = B, si simultáneamente A Í B y B Í A; 

esto equivale a decir que tienen los mismos elementos (o también la misma propiedad característica).

Para cualquier conjunto A se verifica que ÆÍ A y A Í A; 

B Í A es un subconjunto propio de A si A ¹ Æ y B ¹ A.

El conjunto formado por todos los subconjuntos de uno dado A se llama partes de A, y se denota Ã (A). 

Entonces, la relación B Í A es equivalente a decir B Î Ã (A). Ejemplos: 

 

Si A = {a,b} entonces Ã (A) = {Æ ,{a},{b},A}.

Si a Î A entonces {a} Îà(A).

Cuando en determinado contexto se consideran siempre conjuntos que son partes de uno dado U, 

se suele considerar a dicho U como conjunto universal o de referencia.

OPERACIONES ENTRE CONJUNTOS

Dados dos conjuntos A y B, se llama diferencia al conjunto A - B := {a Î A | a Ï B}. 

Asimismo, se llama diferencia simétrica entre A y B al conjunto A D B := (A - B) È (B - A).

Si A Î Ã (U), a la diferencia U - A se le llama complementario de A respecto de U, 

y se denota abreviadamente por A' (U se supone fijado de antemano).

Es fácil ver que si A y B son subconjuntos cualesquiera de U se verifica:

• Æ ' = U .
• U ' = Æ .
• (A')' = A .
• A Í B Û B' Í A' .
• Si A = { x Î U | p(x) es una proposición verdadera} entonces A' = { x Î U | p(x) es una proposición falsa}.

  

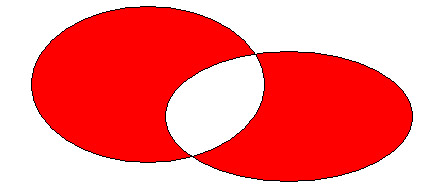
Se llama unión de dos conjuntos A y B al conjunto formado por objetos que son elementos de A o de B, 

es decir: A È B := { x | x Î A Ú x Î B}.

Se llama intersección de dos conjuntos A y B al conjunto formado por objetos que son elementos de A y de B, 

es decir: A Ç B := {x | x Î A Ù x Î B}.

Si A y B son subconjuntos de un cierto conjunto universal U, entonces es fácil ver que A - B = A Ç B'. 

En este caso, la llamadas operaciones booleanas (unión e intersección) verifican las siguientes propiedades :

PROPIEDADES	UNION	INTERSECCION
1.- Idempotencia	A È A = A	A Ç A = A
2.- Conmutativa	A È B = B È A	A Ç B = B Ç A
3.- Asociativa	A È ( B È C ) = ( A È B ) È C	A Ç ( B Ç C ) = ( A Ç B ) Ç C
4.- Absorción	A È ( A Ç B ) = A	A Ç ( A È B ) = A
5.- Distributiva	A È ( B Ç C ) = ( A È B ) Ç ( A È C )	A Ç ( B È C ) = ( A Ç B ) È ( A Ç C )
6.- Complementariedad	A È A' = U	A Ç A' = Æ

 

Estas propiedades hacen que partes de U con las operaciones unión e intersección tenga una estructura de álgebra de Boole. 

Además de éstas, se verifican también las siguientes propiedades:

• A È Æ = A , A Ç Æ = Æ ( elemento nulo ).
• A È U = U , A Ç U = A ( elemento universal ).
• ( A È B )' = A' Ç B' , ( A Ç B )' = A' È B' ( leyes de Morgan ).

  

Dados dos conjuntos A y B, se define el producto cartesiano de ambos como el conjunto de pares ordenados: 

 

A ´ B := { (a,b) : a Î A Ù b Î B}

Dos pares (a,b) y (c,d) de A ´ B son iguales si a = c y b = d; análogamente, dados cuatro conjuntos A,B,C,D se verifica 

 

A ´ B = C ´ D Û ( A = C Ù B = D )

Se llama grafo relativo a A ´ B a todo subconjunto G Í A ´ B. 

Dado un grafo G relativo a A ´ B, se llama proyección de G sobre A al conjunto 

 

Proy_AG := { a Î A : (a,b) Î G, $ b Î B}

Análogamente se define la proyección Proy_BG de G sobre B.

Por último, los conceptos anteriores pueden generalizarse a familias de conjuntos. 

Si para cada elemento i de un conjunto (de índices ) I se tiene un conjunto A_i , entonces se define el conjunto { A_i : i Î I } 

y se denomina familia de conjuntos indicada por I. También se suele denotar por { A_i } _i Î I . 

De forma análoga se define una familia de elementos ( a_i ) _i Î I .

Dada una familia de conjuntos { A_i } _i Î I se definen: 

 

• È _i ÎI A_i := { a : a Î A_i , $ i Î I }
• Ç _i Î I A_i := { a : a Î A_i , " i Î I }
• Õ _i Î I A_i := { (a_i) : a_i Î A_i , " i Î I }

  

Las propiedades de la unión e intersección siguen siendo válidas para familias de conjuntos, y en particular las leyes de Morgan : 

 

( È _i Î I A_i )' = Ç _i Î I A'_i     ,    (Ç_i Î I A_i )' = È_i Î I A'_i

DIAGRAMAS DE VENN

Los conjuntos de suelen representar gráficamente mediante "diagramas de Venn", con una línea que encierra a sus elementos. 

Así, todas las operaciones entre conjuntos se pueden representar gráficamente con el fin de obtener una idea más intuitiva.

A Í B

A È B

 

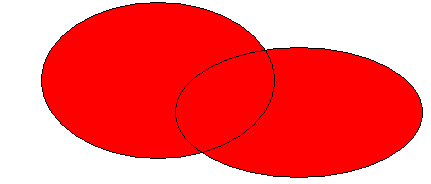
A Ç B

 

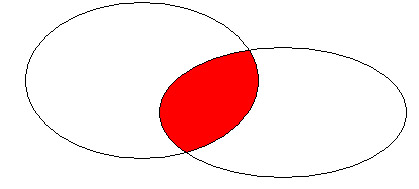
A - B

 

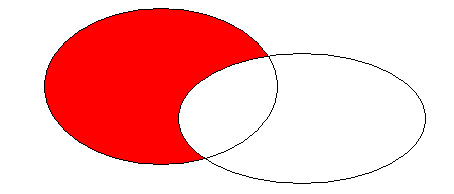
A D B

RELACION ENTRE LA TEORIA DE CONJUNTOS Y LA LOGICA PROPOSICIONAL

Existe una relación muy estrecha entre la Teoría de Conjuntos y la Lógica Proposicional.
Para mostrar dicha relación, denotemos por letras mayúsculas A,B ... los conjuntos y
por las correspondientes minúsculas a,b ... sus propiedades características
(es decir, la proposición lógica que caracteriza a los elementos de cada conjunto);
entonces se tiene la siguiente correspondencia:
 
 

conjuntos	A Í B	A = B	A È B	A Ç B	A'	A - B	A D B
proposiciones	a Þ b	a Û b	a Ú b	a Ù b	a'	a Ù b'	a Ú b

Además, el conjunto vacío se corresponde con una contradicción y el conjunto universal con una tautología.
Mediante esta correspondencia, todos los resultados sobre conjuntos se pueden reescribir en términos de lógica
proposicional y viceversa; a modo de ejemplo:
 
 

A È ( A Ç B ) = A	a Ú ( b Ù c ) Û a
A È ( B Ç C ) = ( A È B ) Ç ( A È C )	a Ú ( b Ù c ) Û ( a Ú b ) Ù ( a Ú c )
( A È B )' = A' Ç B'	( a Ú b )' Û a' Ù b'